Измерения - 4.9. Законы распределения случайных погрешностей.

4.9. Законы распределения случайных погрешностей.

В метрологической практике для описания случайных погрешностей используют ограниченный набор стандартных аппроксимирующих функций распределения (нормальную, равномерную, по треугольнику, по трапеции).

Нормальную функцию распределения имеют следующие случайные величины:

Флуктуационные погрешности разного рода.
Случайные погрешности средств измерений.
Погрешности, складывающиеся из достаточно большого числа (можно считать, что более 5) независимых составляющих при отсутствии доминирующей составляющей.

Равномерные функции распределения имеют:

Погрешности результатов наблюдений, округленных в ближайшую сторону отсчетов с неточностью целого (или долевого) деления шкалы.
Погрешность приближенных вычислений с округлением до ближайшей значащей цифры.
Погрешности регулировки в допустимых пределах ±а.
Люфтовые погрешности.
Погрешности от изменения температуры в допустимых пределах.
Вариация показаний измерительных приборов.

Треугольные функции распределения (по Симпсону) имеют погрешности измерений длины, угла, интервала времени по двум отсчетам (начало-конец).

Аналитические зависимости, области определения, соотношения между параметрами и графики наиболее часто используемых законов распределения представлены в таблице 4.1.

Наиболее распространенной функцией распределения случайной погрешности является нормальная функция (функция Гаусса). При обработке результатов наблюдений при априорно неизвестном законе распределения случайных погрешностей проводят проверку нормальности распределения результатов наблюдений. Для этого используют методы проверки статистических гипотез. Поскольку проверка статистических гипотез основывается на опытных данных, то при принятии решения всегда возможны ошибки.Когда отвергается в действительности верная гипотеза, то совершается ошибка первого рода. Вероятность ошибки первого рода называется уровнем значимости q:

где

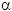- вероятность правильного принятия верной гипотезы.

Когда принимается в действительности неверная гипотеза, то совершается ошибка второго рода. В общем случае вычислить ее вероятность нельзя. Однако при уменьшении вероятности ошибки первого рода вероятность ошибки второго рода увеличивается. Поэтому не имеет смысла выбирать слишком низкий уровень значимости q. Обычно на практике q принимают в пределах (1...5)%. Критерии проверки статистических гипотез приводятся в справочной литературе по теории вероятностей и в нормативных документах по метрологии, в частности, в ГОСТ 8.207 «ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения».