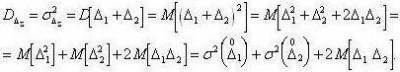Глава
4. Основы теории измерений.
4.10.
Суммирование составляющих погрешности измерений.
Как уже указывалось ранее, погрешности измерения
обуславливаются различными факторами. В связи с этим суммарная случайная
погрешность в общем случае может иметь несколько составляющих. Эту суммарную
случайную погрешность можно оценить, проведя многократные наблюдения. Однако на
практике не всегда можно провести такую серию многократных наблюдений. В этом
случае предварительно оценивают значения математического ожидания и СКО каждой
составляющей погрешности, а оценку суммарной погрешности находят расчетным путем.
Рассмотрим это на примере.
Пусть имеется две составляющие случайной
погрешности измерения. Обозначив индексами «1» и «2» первую и вторую
составляющие случайной погрешности, выразим их математическое ожидание и СКО
следующим образом:
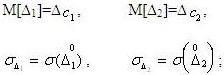
В этом случае математическое ожидание суммарной
погрешности равно:
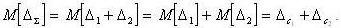
Дисперсия суммарной погрешности определяется
следующим образом:
Математическое ожидание произведения двух случайных
величин (в данном случае - двух случайных погрешностей) называется корреляционным
моментом.
Корреляционный момент определяет степень
«тесноты» линейной зависимости между погрешностями. Вместо корреляционного
момента часто пользуются коэффициентом корреляции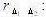 
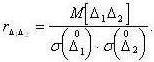
Пользуясь коэффициентом корреляции, можно
записать выражение для дисперсии суммарной погрешности:
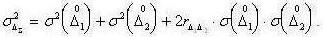
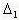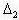Если погрешности  и  некоррелированные, то 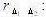= 0, а дисперсия суммарной погрешности определяется по
формуле:
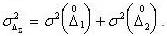
В случае, когда СКО составляющих 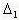и 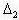неизвестно, то
оценки СКО суммарной погрешности определяют по формуле:
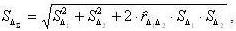
где - 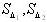 - оценки СКО составляющих 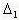и ,
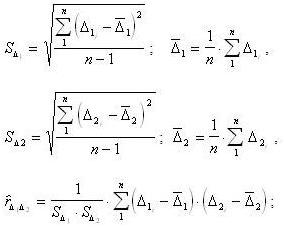
Если 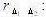>0, то 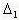возрастает при увеличении .
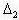Если 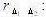<0, то 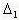уменьшается при
увеличении .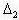
Если 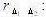=+1, то СКО суммарной погрешности определяется как
сумма СКО первой и второй составляющей,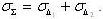 
Если 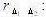= -1, то СКО суммарной погрешности определяется, как
разность СКО первой и второй составляющих,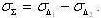 
Если суммарная погрешность имеет m
составляющих, то ее дисперсия равна:
| 
