Глава
4. Основы теории измерений.
4.7.
Точечная и интервальная оценки истинного значения измеряемой физической
величины.
Все бесконечное число значений физической
величины называется генеральной совокупностью. На практике же всегда имеют дело
с ограниченным числом наблюдений или измерений, т.е. имеют дело с выборкой из генеральной совокупности.
Таким образом, оценку точности измерений проводят по ограниченному, хотя иногда
и довольно большому, числу наблюдений. В результате получают одно число. Это
называется точечной оценкой. Задача получения точечных оценок результатов
измерений и СКО случайных погрешностей является частным случаем статистической
задачи нахождения оценки параметров функции распределения случайной величины на
основании выборок - т.е. ряда значений, принимаемых этой случайной величиной в
ограниченном числе n независимых опытов. Независимо от закона
распределения случайной величины, оцениваемыми параметрами является
математическое ожидание и СКО функции распределения. Сами же формулы для оценок
имеют различный вид в зависимости от закона распределения плотности
вероятности. Для нормального закона в формулы для дифференциальной функции
распределения математического ожидания (mx) и СКО 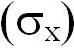 входят в явном виде, а
для равномерного распределения определяются из соотношений: входят в явном виде, а
для равномерного распределения определяются из соотношений:
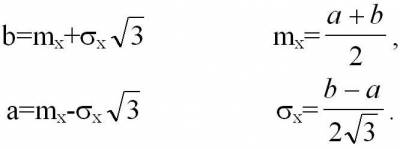
Если есть параметр А, то его оценка 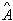 называется
точечной, если она выражается одним числом. называется
точечной, если она выражается одним числом.
Любая точечная оценка, вычисленная на основании
опытных данных, будучи их функцией, сама является случайной величиной с
распределением, зависящим от трех факторов:
закона распределения исходной случайной
величины;
самого оцениваемого параметра;
числа опытов n.
К оценкам предъявляется три требования: - Состоятельность. Оценка считается состоятельной,
если с увеличением числа опытов n она приближается (т.е.
сходится по вероятности) к значениям оцениваемого параметра, т.е.
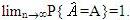 - Несмещенность. Оценка называется
несмещенной, если ее математическое ожидание равно оцениваемому параметру:
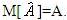 - Эффективность. Оценка называется
эффективной, если ее дисперсия меньше дисперсии другой оценки данного
параметра.
Что значит разные
оценки одного и того же параметра?
Предположим, что имеется упорядоченный или
вариационный ряд результатов наблюдений случайной величины Х:
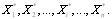
Вариационный ряд - это такой ряд, в котором 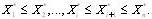 Можно провести оценки различными методами: по
медиане, по размаху, по среднему арифметическому и др.
Что в данном случае понимается под термином
«медиана»?
Медиана Ме[Х] - это центральное среди
результатов наблюдений значение случайной величины в упорядоченном ряду
результатов наблюдений. В случае, когда имеется четное число наблюдений
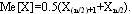
В случае если n нечетное число: 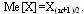
Например: при n=3, 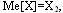 при n=4, при n=4, 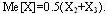
Оценка по размаху: 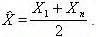
Оценка по среднему арифметическому:
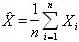
На практике не всегда удается получить оценки
параметров функций распределения случайной величины, удовлетворяющие всем трем
требованиям: состоятельности, несмещенности и эффективности.
Способы получения оценки зависят от закона
распределения случайной величины. Для случайных величин, распределенных по
различным законам, оценки параметров функций распределения проводят по
различным формулам. Существуют различные методы получения оценок. Наиболее
распространенным является метод максимального правдоподобия. Введем
понятие функции правдоподобия, которая зависит от самих результатов наблюдений.
Если Хi результат наблюдений, то функция правдоподобия:
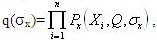 где где
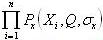 -
произведение. -
произведение.
Для упрощения вычислений пользуются
логарифмической функцией правдоподобия 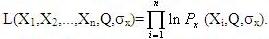
Оценки максимального правдоподобия получают
решением системы уравнений в частных производных:
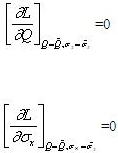
Для нормального распределения случайных величин
или случайных погрешностей оценки максимального правдоподобия следующие:
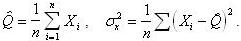
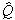 - точечная оценка максимального
правдоподобия. - точечная оценка максимального
правдоподобия.
Однако оценка дисперсии, полученная таким
образом, не является несмещенной. Для получения несмещенной оценки дисперсии
случайной погрешности пользуются следующей формулой:
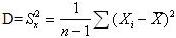
Тогда оценка СКО случайной погрешности,
полученная методом максимального правдоподобия, определяется следующим образом:

где  - несмещенная
оценка генеральной средней, Хi - оценка математического ожидания результатов
наблюдений или результат наблюдений. - несмещенная
оценка генеральной средней, Хi - оценка математического ожидания результатов
наблюдений или результат наблюдений.
Условимся в дальнейшем обозначать оценку
математического ожидания и СКО через 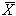 и Sx. Иногда Sx называют стандартом. и Sx. Иногда Sx называют стандартом.
Для равномерного закона распределения
погрешностей
где 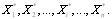 - члены упорядоченного ряда наблюдений
(упорядоченная выборка, - члены упорядоченного ряда наблюдений
(упорядоченная выборка,  ). ).
Достоинствами метода максимального правдоподобия
является то, что полученные оценки:
асимптотически несмещенные (при 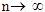 ) )
асимптотически эффективные
асимптотически нормально распределенные.
Т.е. если 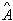 - оценка
максимального правдоподобия параметра А, то при достаточно большом числе
наблюдений (n>25) эта оценка может
считаться нормально распределенной при любом распределении результатов
наблюдений, причем: при - оценка
максимального правдоподобия параметра А, то при достаточно большом числе
наблюдений (n>25) эта оценка может
считаться нормально распределенной при любом распределении результатов
наблюдений, причем: при 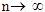  т.е.
эта оценка состоятельная. т.е.
эта оценка состоятельная.
Пример: из генеральной совокупности извлечена
выборка объемом n = 50.
Случайная величина Xi принимает значения: 2, 5,
7, 10; Частность ni 16, 12, 8, 14;
 Найти несмещенную оценку генеральной
средней. Найти несмещенную оценку генеральной
средней.
Несмещенной оценкой генеральной средней является
выборочная средняя 
Таким образом, несмещенная оценка генеральной
средней равна 5,76.
Интервальные оценки параметров функций
распределения погрешностей или результатов наблюдений получают путем
определения интервалов, в границах которых с определенной вероятностью
находятся истинные значения оцениваемых параметров. Такой интервал называется
доверительным, а соответствующая вероятность - доверительной вероятностью.
Доверительный интервал - интервал значений
случайной погрешности, внутри которого с заданной вероятностью находится искомое
(истинное) значение погрешности результатов измерений. Граница доверительного
интервала называют доверительными границами - верхней и нижней.
Если результаты наблюдений или погрешность
результата наблюдений распределены по нормальному закону с известным СКО  то доверительная вероятность нахождения
истинного значения измеряемой величины Q в доверительном интервале то доверительная вероятность нахождения
истинного значения измеряемой величины Q в доверительном интервале  определяется выражением:
определяется выражением:

где Ф(tp) - нормированная
интегральная функция нормального распределения, но поскольку Ф(z)=1-Ф(-z),
т.е. Ф(-z)=1-Ф(z), то

Половина доверительного интервала  называется доверительной
границей случайного отклонения результатов наблюдений, соответствующего
доверительной вероятности Р. Для определения доверительной границы задаются
доверительной вероятностью Р*
(например, Р*=0,95
или Р*=0,
997). называется доверительной
границей случайного отклонения результатов наблюдений, соответствующего
доверительной вероятности Р. Для определения доверительной границы задаются
доверительной вероятностью Р*
(например, Р*=0,95
или Р*=0,
997).
Затем по формулам: 2Ф(tp)-1=Р* определяют
значение Ф(tp) интегральной функции распределения для
нормированного нормального распределения

Определив Ф(tp), по таблицам находят
значение tp, которое зависит от числа измерений,
доверительной вероятности и степени свободы. После этого вычисляют
доверительные границы.
 где символами «В», «Н» обозначаются верхняя и нижняя
границы доверительного интервала, соответственно. где символами «В», «Н» обозначаются верхняя и нижняя
границы доверительного интервала, соответственно.
Проведение многократных наблюдений позволяет
уменьшить доверительный интервал случайной погрешности, поскольку сама
погрешность уменьшается в 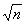 раз. При n
измерениях вероятность раз. При n
измерениях вероятность

где  - оценка
математического ожидания результатов наблюдений по числу наблюдений n. - оценка
математического ожидания результатов наблюдений по числу наблюдений n.
Наблюдение при измерении - операции, проводимые
при измерении и имеющие целью своевременно и правильно провести отсчет
показаний средства измерений.
Измерение - совокупность операций по применению
технического средства, хранящего единицу физический величины с ее единицей с
целью получения значения этой величины (или информации о ней) в форме, наиболее
удобной для дальнейшего использования.
|