Доверительный интервал, полученный по результатам многократных наблюдений, в 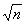 раз меньше интервала, вычисленного по результатам однократного наблюдения измеряемой величины. На этом принципе основан метод снижения случайных погрешностей измерений, т.е. повышения точности результатов измерений. В принципе, увеличение n (числа наблюдений) можно получить сколь угодно малое значение случайной погрешности измерений. Однако на практике, как правило, это весьма сложно (иногда просто невозможно) сделать из-за значительного увеличения времени на проведение измерений. Особо сложно это сделать в быстро изменяющихся процессах. Поэтому необходимо выбирать минимально необходимое число наблюдений для обеспечения такой случайной погрешности, которая была бы не больше допустимой, т.е.  Это число n можно определить из их соотношения

Рассмотрим случай, когда распределение результатов наблюдений соответствует нормальному закону, а дисперсия случайной погрешности  неизвестна. Это наиболее часто встречающееся на практике случай. В этих условиях пользуются следующим отношением:

где S_x - несмещенная точечная оценка СКО, 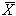 - точечная оценка математического ожидания результатов наблюдений.

Плотность распределения этой дроби описывается дифференциальной функцией распределения Стьюдента:

где S(t, k)- функция распределения Стьюдента, k - число степеней свободы.

Для одной группы измерений k = (n - 1), для j групп по n измерений в каждой группе k = j (n - 1). При интерполяции экспериментальных данных линейной зависимостью y = ax + b по n точкам k = (n - 2),при интерполяции квадратичной зависимостью y = ax² + bx + c по n точкам   k = (n - 3).

Значения  приводится во всех соответствующих справочниках и в ГОСТ 8.207. Этот коэффициент  называется коэффициентом Стьюдента. В этом случае доверительные границы оценки математического ожидания результатов наблюдения определяются по следующим формулам:

Таким образом, при интервальной оценке результат не может быть выражен одним числом. В процессе измерений получают лишь среднее значение измеряемой величины и границы доверительного интервала, внутри которого находится эта измеряемая величина с принятой доверительной вероятностью. Можно сказать, что получают какую-то полосу, внутри которой находятся возможные значения измеряемой величины. Эту полосу называют «дорожкой погрешности» возможных значений Q физической величины с определенной вероятностью.

Рассмотрим пример.

Найти доверительный интервал для оценки с доверительной вероятностью (надежностью) Р=0,95 неизвестного математического ожидания параметра А нормально распределенной случайной величины Х генеральной совокупности, если даны генеральное среднее квадратическое отклонение =5, выборочная средняя =14 и объем выборки n=25.

Надо найти доверительный интервал, в котором находится значение параметра А с заданной доверительной вероятностью (Р=0,95):

Кроме значения t все величины даны. Найдем .

 определяется по таблице значений функции Лапласа.

2Ф(t)=0.95; Ф(t)=0,475.

(в таблице Ф(х) и х)  =1,96. Подставив значение , получим

Назад

Содержание

Вперед