Глава
6. Средства измерений. Классификация средств измерений.
6.3.
Погрешности средств измерений и формы их выражения
Каждое средство измерений обладает определенной
погрешностью. Погрешности СИ определенного типа в реальных условиях применения
может иметь две модели.
Модель I.
Если погрешность СИ соответствует этой модели,
ее суммарная абсолютная погрешность
 (1). (1).
Формула (1) представляет собой символическую
запись объединения составляющих погрешности измерений в реальных условиях
применения, где:
 -
систематическая составляющая основной погрешности СИ; -
систематическая составляющая основной погрешности СИ;
 -
случайная составляющая основной погрешности СИ; -
случайная составляющая основной погрешности СИ;
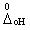 -
случайная составляющая, обусловленная гистерезисом; -
случайная составляющая, обусловленная гистерезисом;
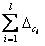 -
объединение дополнительных погрешностей -
объединение дополнительных погрешностей 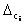 СИ,
обусловленных действием влияющих величин и неинформативных параметров входного
сигнала СИ; СИ,
обусловленных действием влияющих величин и неинформативных параметров входного
сигнала СИ;
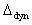 -
динамическая погрешность СИ, обусловленная влиянием скорости (частоты)
изменения входного сигнала СИ; -
динамическая погрешность СИ, обусловленная влиянием скорости (частоты)
изменения входного сигнала СИ;
l - число дополнительных погрешностей.
Модель II.
Если погрешность СИ соответствует этой модели,
ее суммарная абсолютная погрешность
 (2). (2).
Формула (2) представляет собой символическую
запись объединения трех составляющих погрешности СИ в реальных условиях
применения, причем 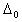 - основная погрешность СИ без разделения ее на
составляющие, как в модели I. - основная погрешность СИ без разделения ее на
составляющие, как в модели I.
В зависимости от свойств СИ данного типа и
реальных условий его применения некоторые или все составляющие 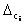 и (или) и (или) 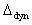 модели II
могут отсутствовать. Число l составляющих модели II
могут отсутствовать. Число l составляющих 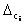 должно быть
равно числу всех величин, существенно влияющих на погрешность СИ в реальных
условиях применения. должно быть
равно числу всех величин, существенно влияющих на погрешность СИ в реальных
условиях применения.
Модель II применима только для СИ
таких типов, у которых случайная составляющая основной погрешности может
считаться несущественной (пренебрежимо малой).
Основная погрешность СИ 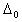 , соответствующего этой модели, определяется следующим
образом: , соответствующего этой модели, определяется следующим
образом:

где 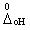 - случайная
составляющая основной погрешности от гистерезиса. - случайная
составляющая основной погрешности от гистерезиса.
Следует отметить, что если составляющие 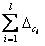 и и 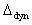 настолько малы,
что их можно не учитывать, т.е. настолько малы,
что их можно не учитывать, т.е.  , то модель II может быть применена и
при наличии существенной случайной составляющей основной погрешности. , то модель II может быть применена и
при наличии существенной случайной составляющей основной погрешности.
Если при применении СИ данного типа допускается,
чтобы погрешность измерений изредка превышала значение, рассчитанное по
нормируемым метрологическим характеристикам СИ, то должна быть выбрана модель I
погрешности СИ. Погрешности СИ могут выражаться:- в
виде абсолютной погрешности
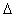 . .
Для меры 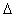 =
Хн - Хд, где Хн - номинальное значение, Хд
- действительное значение измеряемой величины. =
Хн - Хд, где Хн - номинальное значение, Хд
- действительное значение измеряемой величины. Для прибора 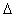 =
Хп - Хд, где Хп - показание прибора; =
Хп - Хд, где Хп - показание прибора;- в
виде относительной погрешности
 - в
виде приведенной погрешности
 где ХN - нормирующее значение
измеряемой ФВ. где ХN - нормирующее значение
измеряемой ФВ.
В качестве нормирующего значения может быть
принят предел измерения данным СИ. Например, для весов с пределом измерения
массы 10 кг. ХN = 10 кг. Если в качестве
нормирующей величины принимается размах всей шкалы, то именно к значению этого
размаха в единицах измеряемой ФВ и относят абсолютную погрешность. Например,
для амперметра с пределами измерения от минус 100 мА до 100 мА ХN = 200
мА. Если в качестве нормирующей величины принимается длина шкалы прибора l, то ХN = l.
На каждое СИ погрешность приводится только в
какой-то одной форме.
Если погрешность СИ при неизменных внешних
условиях постоянна во всем диапазоне измерений, то 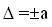 (6.1). Если она
меняется в указанном диапазоне, то (6.1). Если она
меняется в указанном диапазоне, то 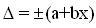 (6.2).
(6.2).
При 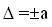 погрешность называется
аддитивной, при погрешность называется
аддитивной, при 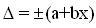 - мультипликативной.
- мультипликативной.
Для аддитивной погрешности  (6.3). (6.3). Для мультипликативной погрешности  (6.4). (6.4).
Приведенная погрешность  (6.5). (6.5).
Значения р, c, d, q, выбираются из ряда
чисел: 1٠10n; 1,5٠10n; (1,6٠10n); 2٠10n; 2,5٠10n; 3٠10n; 4٠10n; 5٠10n; 6٠10n,
где n - положительное или
отрицательное целое число, включая «0».
В зависимости от степени точности СИ им
присваивается класс точности. Общего определения «класс точности» в настоящее
время не существует. Для СИ, у которых погрешность измерения определяется в
соответствии с формулами (6.1) и (6.2) - класс точности присваивается
порядковым номером, начиная для самого точного с 1 и далее по мере возрастания
погрешности.
|