Глава
4. Основы теории измерений.
4.6.
Нормальный закон распределения.
Плотность вероятности или дифференциальная
функция распределения результатов наблюдений, подчиняющихся нормальному закону,
описывается следующей формулой:
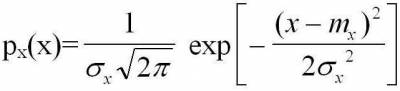 - для результатов наблюдений, - для результатов наблюдений,
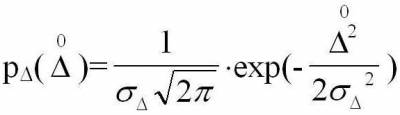 - для случайной погрешности. - для случайной погрешности.
Следует помнить, что 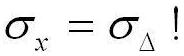
Вероятность попадания результата наблюдения в
заданный интервал 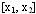 равна: равна:
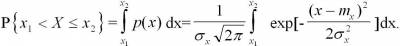
Производя замену переменных 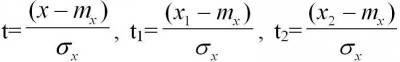 и их подстановку, получим: и их подстановку, получим:
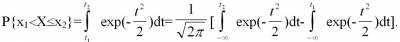
В теории вероятности и метрологии для
определения вероятности попадания наблюдений в некоторый интервал применяется
так называемая нормированная функция Лапласа 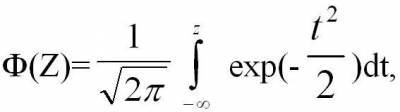 которая табулирована, и
эти таблицы приведены практически во всех литературных источниках по теории
вероятности и метрологии. Используя функцию Лапласа, можно следующим образом
определить вероятность попадания результата наблюдения Х в интервал которая табулирована, и
эти таблицы приведены практически во всех литературных источниках по теории
вероятности и метрологии. Используя функцию Лапласа, можно следующим образом
определить вероятность попадания результата наблюдения Х в интервал 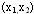 : :
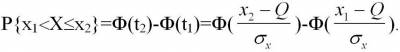
При рассмотрении этой формулы следует иметь в
виду, что: Ф(-Z)=1-Ф(Z).
 Широкое распространение нормального закона в
практике объясняется тем, что распределение случайной погрешности формируется
под воздействием достаточно большого числа случайных независимых факторов,
каждый из которых оказывает лишь незначительное воздействие по сравнению с
суммарным действием всех остальных факторов. Это явление описывается
центральной предельной теоремой (часто называемой теоремой Лапласа). Широкое распространение нормального закона в
практике объясняется тем, что распределение случайной погрешности формируется
под воздействием достаточно большого числа случайных независимых факторов,
каждый из которых оказывает лишь незначительное воздействие по сравнению с
суммарным действием всех остальных факторов. Это явление описывается
центральной предельной теоремой (часто называемой теоремой Лапласа).
Моменты функции распределения случайной
погрешности  , распределенной по нормальному закону: , распределенной по нормальному закону:
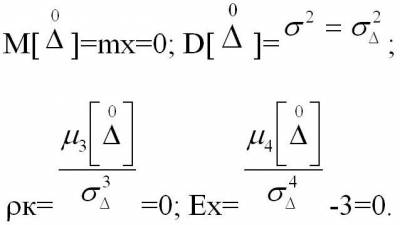
|