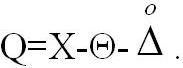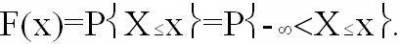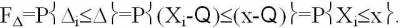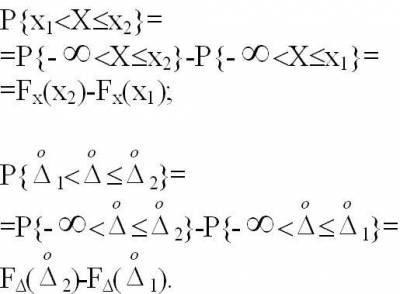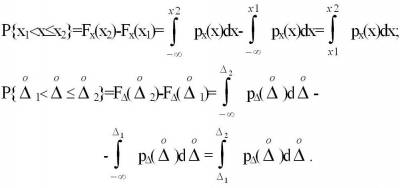Глава 4. Основы теории измерений.
4.3. Интегральная и дифференциальная функции распределения случайных величин и случайных погрешностей.
Рассмотрим результат наблюдения Х постоянной или так называемой детерминированной ФВ Q как случайную величину (СВ), принимающую значения Хi в различных наблюдениях.
В теории вероятностей событие, которое может произойти или не произойти, называется случайным. Количественной оценкой возможности появления данного случайного события является его вероятность. Если имеется всего n событий, а m - число возможных событий, то вероятность появления возможного события Р=m/n. Невозможному событию соответствует вероятность 0, а возможному - 1. Наиболее универсальный способ описания СВ заключается в нахождении их интегральных или дифференциальных функций распределения (ФР).
Интегральной функцией распределения результатов наблюдений является зависимость от величины х вероятности Р того, что результат наблюдений Хi окажется меньше х. Записывается это следующим образом:
Интегральная функция F(x) обладает следующими свойствами:
- F(x) - неубывающая функция.
- F(x)
стремится к 1 при
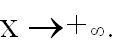
- F(x)
стремится к 0 при
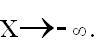
- F(x) - функция непрерывная, т.к. результат наблюдений в определенном интервале может принять любое значение.
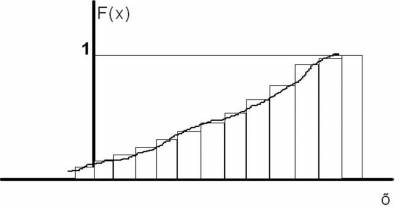
Однако четвертое свойство обычно на практике не реализуется. Это обусловлено тем, что применяемые СИ имеют конечное разрешение: для стрелочного прибора - это цена деления шкалы (квант ФВ), для цифровых приборов - это цена наименьшего разряда кода. Поэтому реально функция распределения для погрешности имеет ступенчатый вид (рис. 4.3.).
Рис.4.3.
Для случайной погрешности, как и для случайной величины, также имеется своя интегральная функция распределения.
Более удобно и наглядно описывать свойство
результатов наблюдений с помощью дифференциальной функции распределения,
которая называется плотностью распределения. Необходимо отметить, что
дифференциальные функции результатов наблюдений Х и случайной погрешности 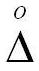 совпадают, только начало координат для
совпадают, только начало координат для 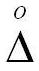 располагается в нулевой точке.
располагается в нулевой точке.
px(x)=dFx(x)/dx - для результатов наблюдений,
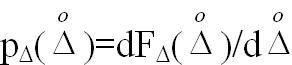 - для погрешности.
- для погрешности.
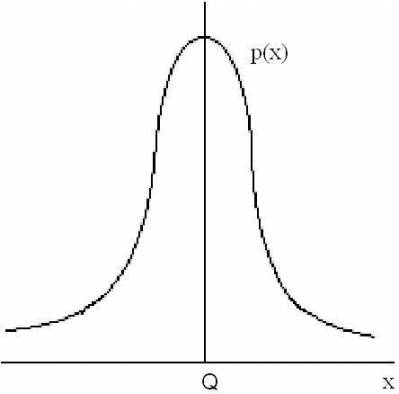
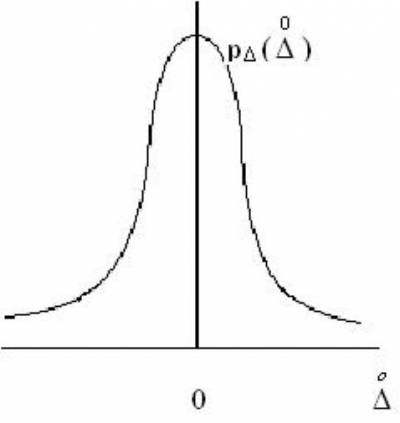
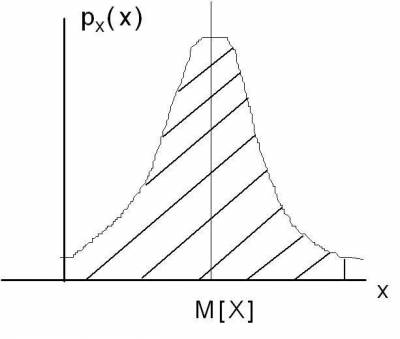
График дифференциальной функции распределения или кривой распределения чаще всего представляет собой симметричную функцию с максимумом в точке «Q» для результатов наблюдений (рис. 4.4.). Кривая распределения для случайной погрешности также чаще всего представляет собой симметричную функцию, но с максимумом в точке «0» (рис. 4.5.).
Рис.4.4.
Рис.4.5.
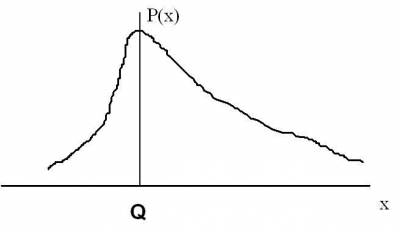
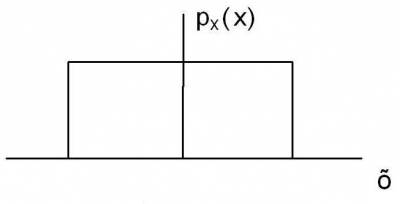
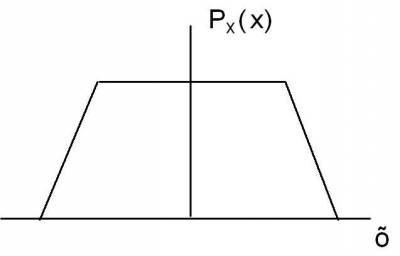
Бывают и несимметричные функции распределения, например, функция Релея (рис. 4.6.) или функции, не имеющие максимума (равномерная или трапециевидная) (рис.4.7., 4.8.).
Рис.4.6.
Рис.4.7.
Рис.4.8.
Интегральная функция связана с дифференциальной следующим образом:
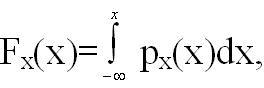 поскольку
поскольку 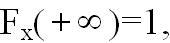 то
то 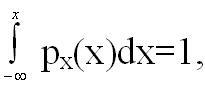 т.е. площадь под кривой
функции распределения равна 1. Это и есть так называемое условие нормировки.
т.е. площадь под кривой
функции распределения равна 1. Это и есть так называемое условие нормировки.
Размерность плотности распределения вероятностей
обратна размерности измеряемой физической величины, т.к. интегральная функция
распределения является безразмерной. Используя понятие функции
распределения, можно получить выражение для вероятности того, что результат
наблюдений находится в полуоткрытых интервалах [x1, x2] или 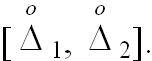
Это выражение говорит о том, что вероятность
попадания результата наблюдения Х или случайной погрешности измерения 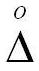 в заданный интервал равна разности значений интегральной функции распределения на указанных
границах этого интервала.
в заданный интервал равна разности значений интегральной функции распределения на указанных
границах этого интервала.
Если выразить эту вероятность через дифференциальную функцию распределения или плотность распределения вероятности, то получим:
Т.е.
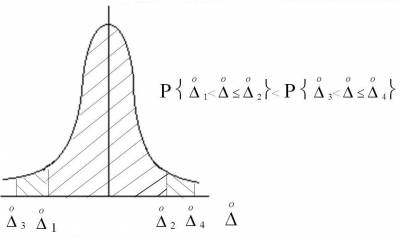
вероятность попадания результата наблюдений Х или случайной погрешности 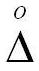 в заданный интервал численно равна площади под
кривой плотности распределения вероятности, ограниченной границами интервала.
в заданный интервал численно равна площади под
кривой плотности распределения вероятности, ограниченной границами интервала.
Рис.4.9.
Произведение px(x)dx называется элементом вероятности. В том случае, когда закон распределения плотности вероятности близок к так называемому «нормальному закону», как видно из графика дифференциальной функции распределения, наиболее вероятны малые значения погрешностей. Вероятность появления больших погрешностей значительно меньше. Результаты наблюдений сконцентрированы вокруг истинного значения измеряемой ФВ, и по мере приближения к нему элементы вероятности возрастают. Это дает основание принять за оценку истинного значения ФВ абсциссу центра тяжести фигуры, образованной осью абсцисс и кривой плотности распределения. Эта характеристика случайной величины называется математическим ожиданием (рис.4.10).
Рис.4.10.
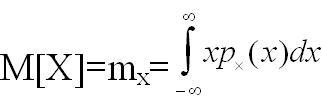
Теперь можно дать математически строгое определение случайной и систематической погрешности.
Систематической
погрешностью ![]() называется отклонение
математического ожидания результатов наблюдений от истинного значения
измеряемой физической величины:
называется отклонение
математического ожидания результатов наблюдений от истинного значения
измеряемой физической величины:
![]()
Случайной
погрешностью 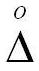 называется разность между результатом
единичного наблюдения и математическим ожиданием результатов наблюдений:
называется разность между результатом
единичного наблюдения и математическим ожиданием результатов наблюдений:
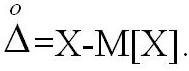
Отсюда истинное значение измеряемой физической величины равно: