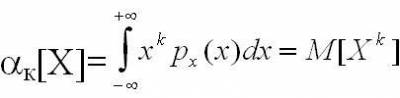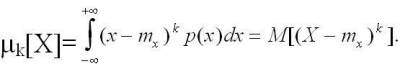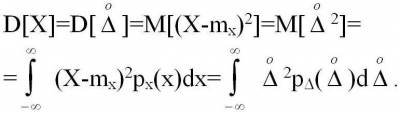Глава 4. Основы теории измерений.
4.4. Моменты функции распределения.
Функция распределения является универсальным способом описания случайной погрешности. Однако чтобы получить ФВ необходимы трудоемкие исследования и расчеты. Поэтому в метрологической практике часто используются характеристики распределения вероятности, называемые моментами.
Начальный момент К-го порядка результатов наблюдений определяется следующим выражением:
Первый начальный момент - математическое
ожидание: 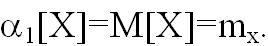
Центральный момент К-го порядка результатов наблюдений определяется по формуле:
В теории измерений важное значение имеет 2-ой центральный момент, называемый дисперсией результатов наблюдений, или дисперсией случайной погрешности:
Дисперсия случайной погрешности является характеристикой рассеяния результатов наблюдений относительно математического ожидания.
Дисперсия имеет размерность квадрата измеряемой физической величины, поэтому значительно чаще в метрологической практике пользуются средним квадратическим отклонением (СКО) результатов наблюдений, являющимся квадратным корнем из дисперсии:
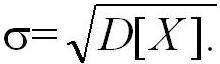
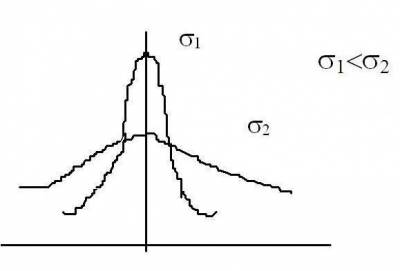
Рис.4.11
Плотность вероятности результатов наблюдений при различных значениях СКО погрешности имеет следующий вид:
Чем больше 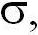 тем более пологой и «расплывчатой» становится
функция распределения. Характеристикой асимметрии функции распределения
является третий центральный момент -
тем более пологой и «расплывчатой» становится
функция распределения. Характеристикой асимметрии функции распределения
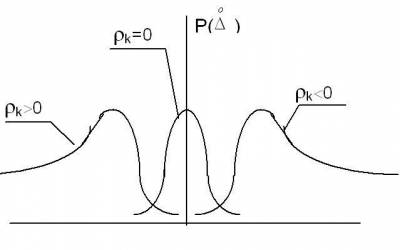
является третий центральный момент - 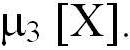 Если ФР симметричная, то все нечетные центральные моменты равны «0» -
Если ФР симметричная, то все нечетные центральные моменты равны «0» - 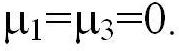 Для удобства в
метрологической практике вводят безразмерную характеристику асимметрии:
Для удобства в
метрологической практике вводят безразмерную характеристику асимметрии: 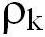 - коэффициент
асимметрии.
- коэффициент
асимметрии.
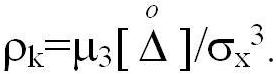
Если 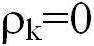 - ФР - симметричная,
если
- ФР - симметричная,
если 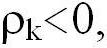 то ее максимум находится в положительной области, если
то ее максимум находится в положительной области, если 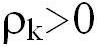 - в отрицательной (см.
рис. 4.12.).
- в отрицательной (см.
рис. 4.12.).
Рис.4.12
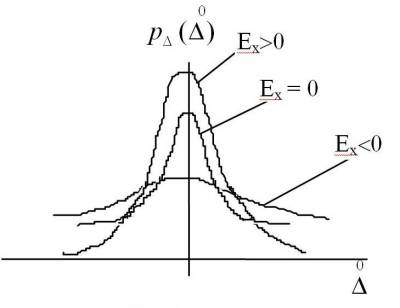
Для определения плосковершинности или
островершинности плотности распределения вероятности случайной погрешности
служит 4-й центральный момент 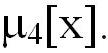 Свойство плосковершинности описывают с помощью эксцесса - безразмерной характеристики, которая определяется
следующим выражением:
Свойство плосковершинности описывают с помощью эксцесса - безразмерной характеристики, которая определяется
следующим выражением: 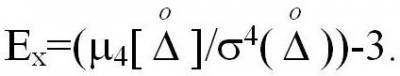 Число 3 вычитается из дроби потому, что
наиболее распространенной в практике измерений функцией распределения плотности
вероятности является распределение по нормальному закону или функция Гаусса.
Число 3 вычитается из дроби потому, что
наиболее распространенной в практике измерений функцией распределения плотности
вероятности является распределение по нормальному закону или функция Гаусса.
Для нормального закона 4-й центральный момент 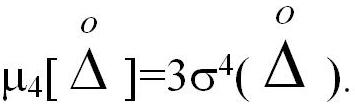 Т.е. для нормального закона распределения Ех=0.
Для более плосковершинного закона распределения Ех<0, для более
островершинного - Ех>0.
Т.е. для нормального закона распределения Ех=0.
Для более плосковершинного закона распределения Ех<0, для более
островершинного - Ех>0.
Моменты распределения используются для идентификации закона распределения результатов наблюдения или их случайной погрешности. В теории и практике наиболее часто встречаются и используются нормальное и равномерное распределение.
Рис.4.13