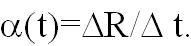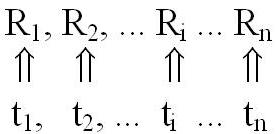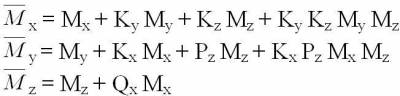Глава 4. Основы теории измерений.

4.2. Виды измерений.

Все измерения могут классифицироваться по:

1. Физической сущности измеряемых ФВ.
2.  Характеристике точности - равноточные, неравноточные.
3. Числу измерений случайной величины - однократные, многократные.
4. По отношению к определяемой величине по времени - статические, динамические.
5. Метрологическому назначению - технические, метрологические.
6. Выражению результата измерений - абсолютные, относительные.
7. Общим приемам получения результатов наблюдений, (по способу получения числового значения ФВ) - прямые, косвенные, совместные, совокупные.

Равноточные измерения - ряд измерений какой-либо величины, выполненных одинаковыми по точности СИ и в одних и тех же условиях.

Неравноточные измерения - ряд измерений  какой-либо величины, выполненных несколькими различными по точности СИ и (или) в разных условиях.

Однократное измерение - измерение, выполненное один раз.

Многократные измерения - измерения одного и того же размера ФВ, результат которого получен из нескольких следующих друг за другом наблюдений, т.е. состоящих из ряда однократных измерений.

Прямое измерение - измерение ФВ, проводимое прямым методом, при котором искомое значение ФВ получают непосредственно из опытных данных. Прямое измерение производится путем экспериментального сравнения измеряемой ФВ с мерой этой величины или путем отсчета показаний СИ по шкале или цифровому прибору. (Для примера: измерения с помощью линейки, вольтметра, весов).

Уравнение прямого измерения: Q=q[Q].

Косвенное измерение - измерение, проводимое косвенным методом, при котором искомое значение ФВ находят на основании результата прямого измерения другой ФВ, функционально связанной с искомой величиной известной зависимостью между этой ФВ и величиной, получаемой прямым измерением.

Уравнение косвенных измерений имеет вид:

Y=F(x₁,x₂,...,x_i,...,x_n); Y=F(x),

где F - известная функция; n - число прямых измеренных ФВ; х₁, х₂,...х_i,...х_n - значения прямо измеренных ФВ.

Например: определение площади, объема, электрической мощности методом измерения силы тока I и напряжения U, коэффициента полезного действия.

Совокупные измерения - проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях различных сочетаний этих величин.

Пример 1: Значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь.

Имеются гири с массами m₁, m_2, m₃,.

 

 

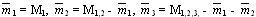
М_1,2 - масса гирь m₁ и m₂;  М_1,2,3 - масса гирь m₁, m_2, m₃;  М_1,3 - масса гирь m₁ и m₃.

Часто именно этим путем добиваются повышения точности результатов измерений.

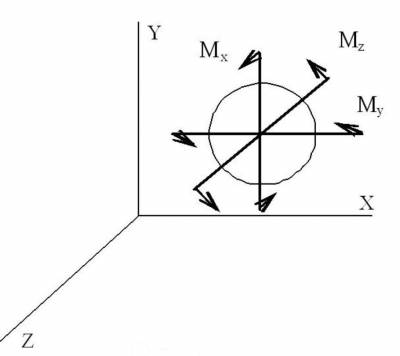
Пример 2: Градуировка трех компонентных весов для измерения трех моментов М_х, М_y, M_z. (Рис.4.2.).

Рис.4.2.

 

Весы нагружаются тремя моментами силы M_x, M_y и M_z. Необходимо найти значения моментов 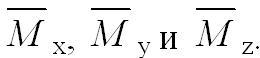Они определятся из уравнений, полученных путем решения системы из шести уравнений, в которых не учитываются величины третьего и больше порядка малости:

 

Совместные измерения - проводимые одновременно измерения двух или нескольких неодноименных физических величин для определения зависимости между ними.

Пример 1. Построение градуировочной характеристики y=f(x) измерительного преобразователя, когда одновременно измеряются наборы значений:

 

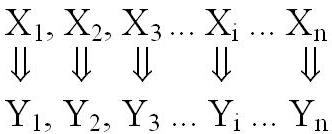
Пример 2. Определение температурного коэффициента сопротивления (ТКС) путем одновременного измерения сопротивления R и температуры 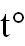, а затем определение зависимости

 

Назад

Содержание

Вперед