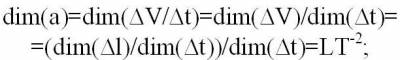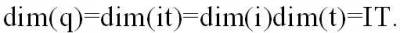Глава 2. Физическая
величина. Системы единиц физических величин.
2.1. Физическая
величина.
Как уже было сказано выше, ФВ - это свойство, общее в качественном отношении многим физическим объектам (физическим системам, их состояниям и происходящим в них процессам), индивидуальное в количественном отношении для каждого объекта.
Индивидуальность в количественном отношении следует понимать в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого.
Термин «величина» обычно применяется в отношении тех свойств или характеристик, которые могут быть оценены количественно, т.е. могут быть измерены. Существуют такие свойства или характеристики, которые в настоящее время наука и техника еще не позволяют оценивать количественно, например, запах, вкус, цвет. Поэтому такие характеристики обычно избегают называть «величинами», а называют «свойствами».
В широком смысле «величина» - понятие многовидовое. Это можно продемонстрировать на примере трех величин.
Первый пример - это цена, стоимость товаров, выраженная в денежных единицах. Раньше системы денежных единиц были составной частью метрологии. Сейчас - это самостоятельная область.
Вторым примером разновидности величин можно назвать биологическую активность лекарственных веществ. Биологическая активность ряда витаминов, антибиотиков, гормональных препаратов и т.п. выражается в Международных единицах биологической активности, обозначаемых И.Е. (Например, в рецептах пишут «количество пенициллина - 300 тыс. И.Е.»).
Третий пример - физические величины, т.е. свойства, присущие физическим объектам (физическим системам, их состояниям и происходящим в них процессам). Именно этими величинами, главным образом, и занимается современная метрология.
В тех случаях, когда необходимо подчеркнуть, что речь идет о количественном содержании в данном объекте физической величины, следует употреблять слово «размер». Количественная оценка конкретной физической величины, выраженная в виде некоторого числа единиц данной величины, называется значением физической величины. Отвлеченное число, входящее в значение физической величины, называется числовым значением. Между значением и размером величины есть принципиальная разница. Размер величины существует реально, независимо от того, знаем ли мы его, или нет. Выразить размер величины можно при помощи любой единицы.
Размер ФВ, обозначаемый Q, не зависит от выбора
единицы, однако числовое значение целиком зависит от выбранной единицы. Если
размер величины Q в системе единиц ФВ (1) определится как Q= n1
[Q1], где [Q1] - единица ФВ в
системе (1), n1 - числовое значение
размера ФВ в этой же системе, то в другой системе единиц ФВ (2), в которой [Q2] не равно [Q1], не изменившийся
размер Q будет выражен другим
значением Q = n2
[Q2], но при этом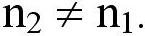 
Так, например масса
одного и того же батона хлеба может быть 1кг или 2,5 фунта, или диаметр
трубы Д=20'=50,8
см.
Поскольку размерность ФВ представляет собой
выражение, отражающее связь с основными величинами системы, в которой
коэффициент пропорциональности равен 1, то размерность равна произведению
основных ФВ, возведенных в соответствующую степень. Например, в системе LMT
размерность производной единицы равна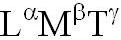 
. Записывается это
следующим образом:
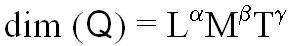
(dim от слова «dimension»
- размерность), это определяет размерность производной величины Q относительно основных
величин L,M,T. Размерность
производной величины отражает, во сколько раз изменится ее размер при изменении
размеров основных величин. Например, если величина Х равна 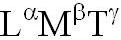, и длина изменяется от l до
l1, а масса - от m до m1, время - от t до
t1, то новый размер величины Х' изменится по сравнению
с прежним в 
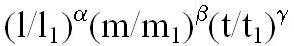раз.
Вычисление размерности существенно упрощается, если учесть, что при этом выполняется следующие два правила:
Если P = RQ, то dim(P)=dim(R) × dim(Q).
Если P=R/Q, то dim(R)= dim(R)/dim(Q),
где Р, R и Q - любые физические величины.
Например, размерность:
ускорения –
электрического заряда-
В общем случае, формула размерности для единиц ФВ имеет вид:
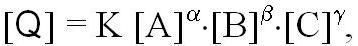
где К - некоторое постоянное число.
Если единицы [A], [B] и [C] являются основными, то эта формула определяет размерность производной единицы [Q] относительно основных единиц. Эта формула показывает размерность производной единицы, но ничего не говорит о размере единицы, поскольку множитель К не определен. Коэффициент К желательно выбрать таким, чтобы уравнения связи между величинами формально совпали с уравнениями связи между их числовыми значениями. При этом вычисления по уравнениям физики значительно упрощаются, и снижается риск допустить ошибки в расчетах. Для этого достаточно положить К=1. Тогда производные единицы определяются следующим образом:
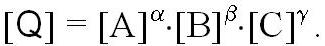
Системы единиц, производные единицы которых образуются по выше приведенной формуле, называются согласованными или когерентными. Понятие размерности широко используется в физике, технике и метрологической практике при проверке правильности сложных расчетных формул и выяснении зависимости между ФВ.
На практике часто бывает необходимо использовать безразмерные величины.
Безразмерная ФВ - это величина, в размерность которой основные величины входят в степени, равной 0. Однако следует понимать, что величины, безразмерные в одной системе единиц могут иметь размерность в другой системе. Например, абсолютная диэлектрическая проницаемость в электростатической системе является безразмерной, в то время как в электромагнитной системе ее размерность равна L-2 T2, а в системе LMTI ее размерность - L-3 M-1 T4 I2.
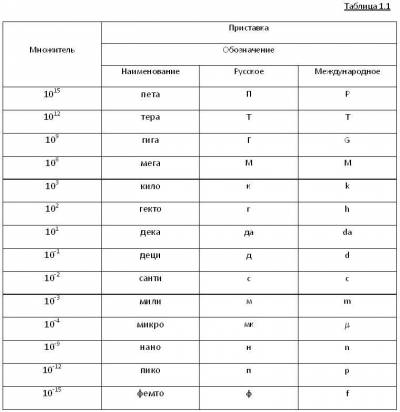
Единицы той или иной физической величины, как правило, связаны с мерами. Размер единицы измеряемой физической величины принимается равным размеру величины, воспроизводимому мерой. Но на практике одна единица оказывается неудобной для измерения больших и малых размеров данной величины. Поэтому применяется несколько единиц, находящихся в кратных и дольных соотношениях между собой.
Кратная единица ФВ - единица, которая в целое число раз больше, чем основная или производная единица.
Дольная единица ФВ - единица, которая в целое число раз меньше основной или производной единицы.
Кратные и дольные единицы ФВ образуются благодаря соответствующим приставкам к основным единицам. Эти приставки приведены в таблице 1.1.
